A Note On The Sampling Principle For Continuous Signals Pdf

Sampling Of Continuous Time Signals Pdf Sampling Signal Processing One way of characterizing the sampling process is achieved by analyzing the relationship between the fourier transform of the continuous and discrete signals. there are many ways of nding the relationship between the two fourier transforms. Basic guiding principles: given a discrete time signal s[n], a good interpolation method should produce a continuous time signal s(t) such that (a) s(t) has s[n] as its samples, i.e. s(nts) = s[n], for each n (b) s(t) is as smooth as possible.

Sampling Of Analog Signals Pdf Sampling Signal Processing Two sampling (integral interpolation) theorems for continuous signals (continuous parameter stochastic processes) are proved. the first of these is the sampling principle introduced by shannon, precise formulation or proof of which has not appeared hitherto. 1 in this lecture, we will examine two important topics in signal processing: . 1.sampling– the process of converting a continuous time signal to discrete time signal so that computers can process the data digitally. Lecture 8 sampling in one dimension 8.1 learning objectives describe the mathematical formulation for sampling a continuous signal. recognize the connection between sampling in one domain, and generating replicas in its fourier transform domain. recognize the risk of aliasing, and the sampling rate (nyquist) required to avoid it. In principle, the continous time signal is reconstructed by placing a suitable pulse at each sample location and adding all pulses. the amplitude of each pulse is given by the sample value. p(t ⇢ 1 for ts 2 t ) = 0 else. else. nts ). add all pulses to obtain the reconstructed signal. reconstruction with the above pulses will be pretty good.

Signals Sampling Theorem Pdf Sampling Signal Processing Lecture 8 sampling in one dimension 8.1 learning objectives describe the mathematical formulation for sampling a continuous signal. recognize the connection between sampling in one domain, and generating replicas in its fourier transform domain. recognize the risk of aliasing, and the sampling rate (nyquist) required to avoid it. In principle, the continous time signal is reconstructed by placing a suitable pulse at each sample location and adding all pulses. the amplitude of each pulse is given by the sample value. p(t ⇢ 1 for ts 2 t ) = 0 else. else. nts ). add all pulses to obtain the reconstructed signal. reconstruction with the above pulses will be pretty good. This low pass reconstruction filter sin is also called the interpolation filter, as it interpolates the signal between samples. This document summarizes and proves two sampling theorems for continuous signals (continuous parameter stochastic processes): 1. the sampling principle of shannon is proved. it states that a continuous signal with a spectral density vanishing outside an interval can be reconstructed from samples taken at twice the maximum frequency. 2. For sampling, three fun damental issues are (i) how are the discrete time samples obtained from the continuous time signal?; (ii) how can we reconstruct a continuous time signal from a discrete set of samples?; and (iii) under what conditions can we recover the continuous time signal exactly?. This is the conceptual content of the sampling theorem (nyquist 1928; shannon 1948, 1949)2 that is enunciated as follows: “a continuous time signal that does not contain frequency components f.

06 Sampling Of Continuous Time Signals Pdf Eece 5666 Digital Signal This low pass reconstruction filter sin is also called the interpolation filter, as it interpolates the signal between samples. This document summarizes and proves two sampling theorems for continuous signals (continuous parameter stochastic processes): 1. the sampling principle of shannon is proved. it states that a continuous signal with a spectral density vanishing outside an interval can be reconstructed from samples taken at twice the maximum frequency. 2. For sampling, three fun damental issues are (i) how are the discrete time samples obtained from the continuous time signal?; (ii) how can we reconstruct a continuous time signal from a discrete set of samples?; and (iii) under what conditions can we recover the continuous time signal exactly?. This is the conceptual content of the sampling theorem (nyquist 1928; shannon 1948, 1949)2 that is enunciated as follows: “a continuous time signal that does not contain frequency components f.
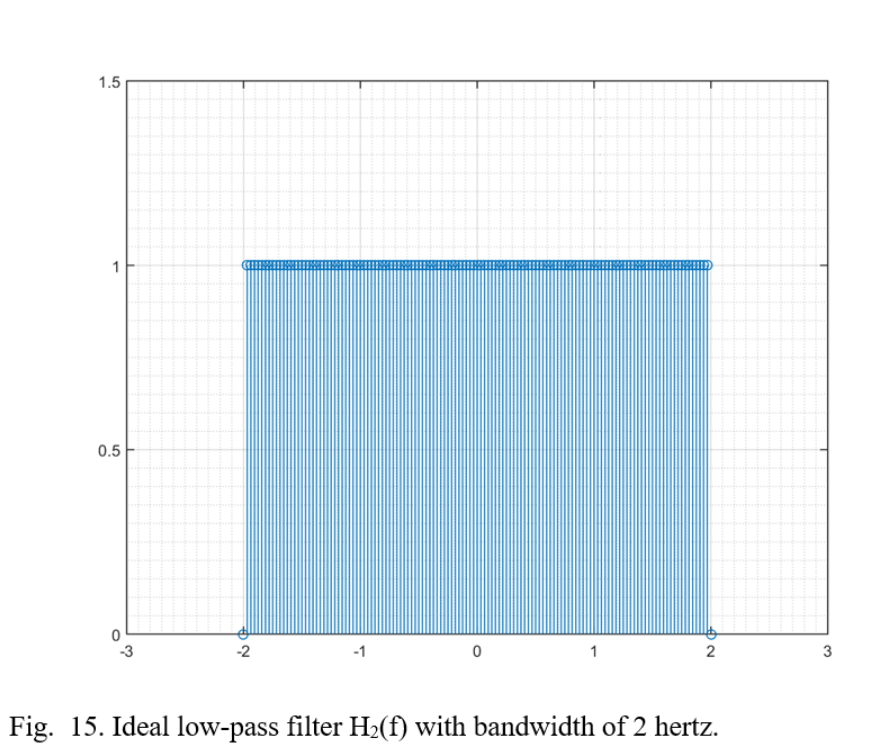
Sampling Continuous Signals Zack S Lab For sampling, three fun damental issues are (i) how are the discrete time samples obtained from the continuous time signal?; (ii) how can we reconstruct a continuous time signal from a discrete set of samples?; and (iii) under what conditions can we recover the continuous time signal exactly?. This is the conceptual content of the sampling theorem (nyquist 1928; shannon 1948, 1949)2 that is enunciated as follows: “a continuous time signal that does not contain frequency components f.
Comments are closed.