10 If A2 B C3 D2 256 And The Value Of 2 A B 3 Studyx

10 If A2 B C3 D2 256 And The Value Of 2 A B 3 Studyx If $a^ {2} b c^ {3} d^ {2}=256$ and the value of $2 a b 3 c$ $ 2 \mathrm {~d}$ is minimum possible, where $\mathrm {a}, \mathrm {b}, \mathrm {c}$ and d are positive real numbers, then find the value of $ (a 2 b 3 c 4 d)$. Solve an equation, inequality or a system. what can quickmath do? quickmath will automatically answer the most common problems in algebra, equations and calculus faced by high school and college students. the algebra section allows you to expand, factor or simplify virtually any expression you choose.

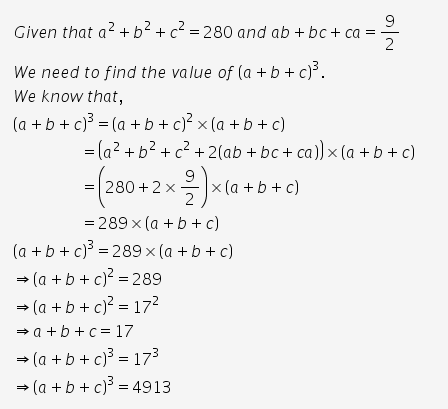
If A2 B2 C2 280 And Ab Bc Ca 9 2 Find The Value Of A B C 3 This result is derived by maximizing the product \ (abcd\) under the constraint \ (a 2b 3c 4d = 50\) using the am gm inequality, and then substituting this maximum value into the given expression. Solution: a b c=10 squaring both sides => (a b c)² = 10² => a² b² c² 2 (ab bc ca) = 100 => 38 2 (ab bc ca) = 100 => 2 (ab bc ca) = 62 => ab bc ca = 31 a³ b³ c³ 3abc = (a b c) (a² b² c² ab bc ca) =>160 3abc = (10) ( 38 31) => 3abc = 160 70 => 3abc = 90 => abc = 30 abc = 30. To solve the expression a2 b2 a3−b3 given the equations a b= 8 and a−b= 2, we can follow these steps: to find the values of a and b, we can add these two equations together: (a b) (a−b) = 8 2. this simplifies to: 2a = 10. dividing both sides by 2 gives: a = 5. now, we can substitute a back into one of the original equations to find b. using a b= 8:. Find the greatest value of $a^2\cdot b^3$ where $a,b$ are positive real numbers satisfying $a b=10$. determine the values of $a,b$ for which the greatest value is attained.

Solved D If A 3 And B 2 Find The Values Of I A 2 2ab B 2 And A To solve the expression a2 b2 a3−b3 given the equations a b= 8 and a−b= 2, we can follow these steps: to find the values of a and b, we can add these two equations together: (a b) (a−b) = 8 2. this simplifies to: 2a = 10. dividing both sides by 2 gives: a = 5. now, we can substitute a back into one of the original equations to find b. using a b= 8:. Find the greatest value of $a^2\cdot b^3$ where $a,b$ are positive real numbers satisfying $a b=10$. determine the values of $a,b$ for which the greatest value is attained. Given a b=10 we know (a b)^2=a^2 b^2 2ab 10^2=58 2ab 2ab=100−58=42 ab=21 (a b)^3=a^3 b^3 3ab (a b) 10^3=a^3 b^3 3×21×10 a^3 b^3=1000−630=370. Question answered step by step if $\frac {a^ {2} b^ {2} c^ {2} 256} {a b b c c a}= 2$ and $a=3 c b$, where $c>0$ then the value of $c$ is : a. 16 · · · copy link. First, recall the algebraic identity for the difference of squares: a2−b2=(a b)(a−b) using the given a2−b2=c and a b=d, we can substitute a b with d: d(a−b)=c. Given: a b c=10a2 b2 c2=50abc=9. using the identity: (a b c)2=a2 b2 c2 2(ab bc ca) substitute the known values: 102=50 2(ab bc ca)100=50 2(ab bc ca)50=2(ab bc ca)ab bc ca=25. now substitute all known values into the identity: a3 b3 c3=(a b c)(a2 b2 c2−ab−bc−ca) 3abca3 b3 c3=10(50−25) 3⋅9a3 b3 c3=10⋅25 27a3 b3 c3=250 27a3 b3 c3=277. a3 b3 c3=277.