%e3%80%90pre Calculus%e3%80%91function Growth Rates

Growth Rates Of Functions Calculus I We say f f and g g grow at the same rate as x → ∞ x → ∞. next we see how to use l’hôpital’s rule to compare the growth rates of power, exponential, and logarithmic functions. It involves calculating average and instantaneous growth rates using differences and derivatives, comparing long term behavior, and exploring the remarkable growth rates of exponential functions.

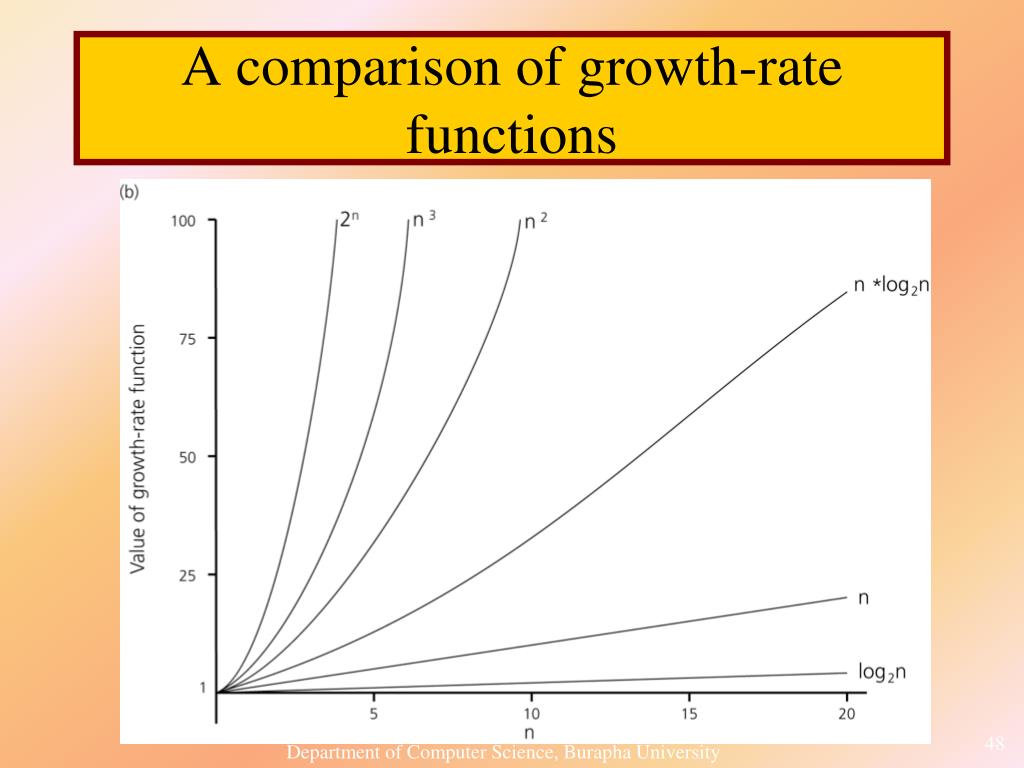
Growth Rates Of Functions Calculus I This video goes over growth rates of functions and how that affects them. the specific application is about end behavior of functions and potential asymptot. We will use something called big o notation (and some siblings described later) to describe how a function grows. what we're trying to capture here is how the function grows. … without worrying about what happens for small inputs: they should always be fast. |f(x)| ≤ c|g(x)| for all x> k. Here is a table that shows some input and output values of an exponential function g g. the equation g(x) = 3x g (x) = 3 x defines the function. 1. how does g(x) g (x) change every time x x increases by 1? show or explain your reasoning. the output values increase by a factor of 3. Moreover, if b = 1 r, we call r the growth rate. whenever b> 1, we often say that the function f is exhibiting “exponential growth”, wherease if 0

7 8 Related Rates Of Growth Here is a table that shows some input and output values of an exponential function g g. the equation g(x) = 3x g (x) = 3 x defines the function. 1. how does g(x) g (x) change every time x x increases by 1? show or explain your reasoning. the output values increase by a factor of 3. Moreover, if b = 1 r, we call r the growth rate. whenever b> 1, we often say that the function f is exhibiting “exponential growth”, wherease if 0 0. is called the coefficient and is called the base. exponential functions do not have a constant growth rate. let with domain . each time we moved in the domain, did not increase by the same amount. From this, we can set up an exponential function, with our initial amount of $ 1000 and a growth rate of r = 0.001 and our input m measured in months: f (m) = 1000 (1 0.012 12) m = 1000 (1.001) m. after 24 months, the account will have grown to f (24) = 1000 (1.001) 24 ≈ $ 1024.28. It says that a quantity that grows exponentially has a constant relative growth rate. constant relative growth rate, or constant percent change, is the hallmark of exponential growth.

Solved An Alternative Way Of Computing Growth Rates In Chegg Growth of functions is a mathematical concept that deals with the rate at which a function increases as its input increases. it is used to compare the efficiency of algorithms and to determine the time complexity of algorithms. the most commonly used growth functions are logarithmic, linear, polynomial, exponential, and factorial. Exponential functions are those functions that experience a constant percentage growth rate. their formulas look like. where a ≠ 0 and r> 0. is called the coefficient and is called the base. exponential functions do not have a constant growth rate. let with domain . each time we moved in the domain, did not increase by the same amount. From this, we can set up an exponential function, with our initial amount of $ 1000 and a growth rate of r = 0.001 and our input m measured in months: f (m) = 1000 (1 0.012 12) m = 1000 (1.001) m. after 24 months, the account will have grown to f (24) = 1000 (1.001) 24 ≈ $ 1024.28. It says that a quantity that grows exponentially has a constant relative growth rate. constant relative growth rate, or constant percent change, is the hallmark of exponential growth.
Growth Function Hot Sex Picture From this, we can set up an exponential function, with our initial amount of $ 1000 and a growth rate of r = 0.001 and our input m measured in months: f (m) = 1000 (1 0.012 12) m = 1000 (1.001) m. after 24 months, the account will have grown to f (24) = 1000 (1.001) 24 ≈ $ 1024.28. It says that a quantity that grows exponentially has a constant relative growth rate. constant relative growth rate, or constant percent change, is the hallmark of exponential growth.
Comments are closed.